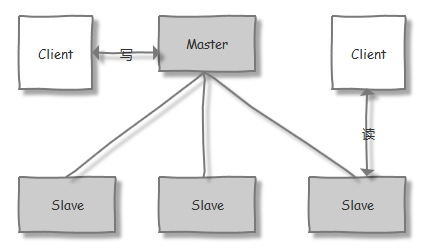
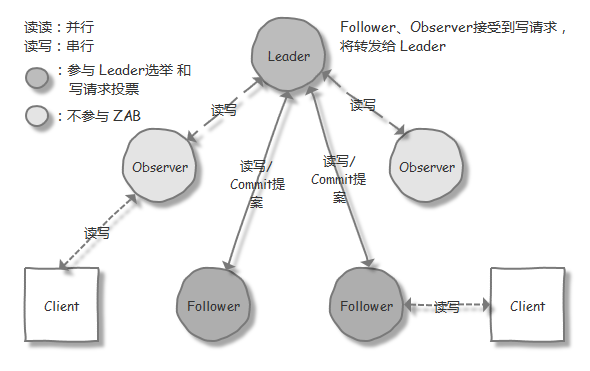
人工智能
什么是人工智能
人工智能(Artificial Intelligence, AI)亦称机器智能,是指由人工制造出来的系统所表现出来的智能。 — wikipedia.org
从深蓝到 AlphaZero,再到 StyleGAN 和 GPT,人工智能的智力水平、学习能力和普适性,正在以爆炸式地速度快速发展;
从棋类到医学,再到绘画和聊天,人工智能开始在各类应用领域大展身手;
从 CPU 到 GPU,再到 TPU 和 IPU,人工智能的计算能力正向着无法穷举的极限不断逼近 …
但是,我们并不浮躁,踏踏实实地点亮 AI 知识树的每个枝叶,才是我们每位富有科学精神的人所应该做的
关于本文
我们将分为三块对 AI 进行诠释
首先,将介绍人工智能的主流思想和实用技巧,通过一些耳熟能详的有趣定理,我们可以对人工智能有些直观、初步的认识;随后,言归正传,我们将开始接触 AI 领域的几大理论支柱,由浅入深地学习 统计学、微积分、线性代数、概率论 等知识体系;最后,落地到实践,我们需要紧跟人工智能的技术发展前沿,对重大的突破性项目进行了解、学习,以及运用。如此,对人工智能领域进行横向分层,可以很方便地找到我们学习的突破点
不过,出于文章编排的考虑,可能部分编码就要放在其他博文中了,如有不便,还望见谅(Python、Prolog、R、Java)。本文持续更新中,若有不妥之处,还请不吝赐教哈 (^o^)/
主流思想
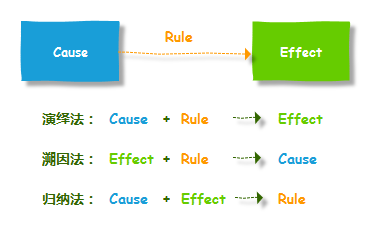
演绎法 & 溯因法 & 归纳法
实用技巧
Occam 剃刀原理
奥卡姆剃刀(Occam´s Razor),意为简约之法,是由 14 世纪逻辑学家、圣方济各会修士奥卡姆的威廉提出的一个解决问题的法则,即"切勿浪费较多资源,去做'用较少的资源,同样可以做好'的事情",相同思想见于郑板桥的删繁就简三秋树